Shear Stress in Physics: Formula, Calculate, and Applications

Shear stress, or tangential stress, occurs when forces cause material layers to slide parallel to each other. Essential in physics and engineering, it helps predict deformation and failure in materials. This blog covers its definition, formulas, and real-world applications.

What is Shear Stress?

Shear stress is a type of stress which occurs when the applied force is tangential to the surface on an object. During shear stress, the force is applied on the planes within the material and that force causes these planes to slide over each other. The following figure represents the shear stress:

Shear stress symbol

Shear stress is expressed with the symbol “Ꚍ”. It is pronounced by tau.

Shear Stress Formula

Here,

Ꚍ = shear stress

F = Applied Force

A = Area under the force

Shear stress units

The unit for shear stress is the same as for stress i.e. Pa. It is equal to N/m².

Shear Stress Example

Shear stress is involved in almost every activity in a day. Some examples such as chewing the gum between the teeth. The force is applied in a parallel direction to the surface, so the planes slide over each other. Shear stress causes the cards to slide over each other as shown in the following figure.

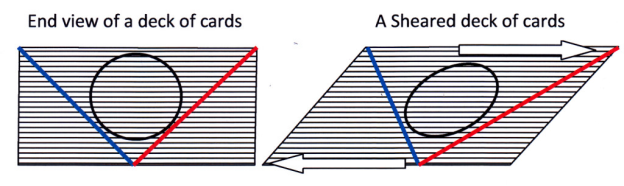
What is shear load

The force is applied to a specimen tangent on the loading axis but not through the centre of the specimen. The load acts perpendicularly on the specimen. Such forces tend to cause a horizontal sliding failure in the applications. In the case of bending, a shear load is applied so as a result shear stress occurs.

Shear Stress in Solid Mechanics

Shear stress in solid mechanics is the internal resistance to the applied shear load. It is very important for the analysis of beams, shafts etc. and material deformation.

Shear Stress in Elastic and Plastic Deformation

In elastic deformation, shear stress causes temporary deformation which means the material can get back to its original position.

Ꚍ = G.γ

G is the Shear Modulus and γ is the shear strain.

While in plastic deformation, shear stress causes permanent deformation.

How to Calculate Shear Stress

To calculate shear stress, the force which causes the planes to slide over each other and the area under that force is needed to calculate first. For instance, if 50N is applied on a plate of 0.03 m³ area, then the shear force will be

Shear stress equation

Ꚍ = 1666 Pa= 1.6 KPa

Viscosity and Shear Stress

Viscosity opposes the flow of the liquid. It is resistance to the movement of particles of the liquid or a change in their shape. For instance, water has a low viscosity of 1mPas which means its shape can be easily changed or it flows fast because of very low viscosity.

Viscosity is the resistance to the change in material due to applied shear stress.

Transverse Shear Stress

Due to bending, produced shear stress is considered as transverse shear stress. It often occurs in the beams due to perpendicularly applied load.

Shear Stress vs Normal Stress

The force applied to the surface at 90^o to the surface causes normal stress while the force tangential to the surface produces shear stress in the body.

Tensile Stress vs. Shear Stress

Tensile stress is the internal resistance to the pulling or stretching force i.e. perpendicular force to the surface of an object.

If the force is applied parallel to the cross-section, then the generated stress is shear stress.

Shear Stress vs. Shear Strength

These terms are interrelated to each other. Shear stress occurs because of tangentially applied forces to the surface. Shear strength is the ability of the body to resist the deformation which will be produced because of shear stress.

How to Find Shear Stress

Calculate the applied force (F) and cross-sectional (A) area to find shear stress.

Methods of Measuring Shear Stress

To measure shear stress theoretically, Mohr’s circle (graphical method) is used. While practically there are different techniques to measure shear stress. In most labs, strain gauges are applied to the specimen under the shear stress. The strain gauge shows the value of shear stress as it deforms with the specimen.

Impact of Shear Stress on Materials

Shear stress leads to structural defects such as delamination in laminated composites, buckling of beams and disbanding of adhesive plates. Ultimately, shear stress causes failure of products.

Shear stress of steel

It depends on the grade, type, shear rate etc. but for mild steel, shear stress is 150MPa and for high-strength steel is 420 MPa.

Shear stress of aluminium

The shear stress of pure aluminum is 30 MPa while for an alloy for instance 6061 Al, the shear stress is 150 MPa.

Shear stress of titanium

Ti is one of the strongest materials and shows relatively higher shear stress than other materials, for example, the shear stress for Ti-3Al-2.5V is 360 MPa.

Shear Stress in Engineering Applications

It is important to have information related to shear stress in engineering applications as it decides the failure criteria for materials. For instance, shear stress provides information like how much shear load will cause failure such as in crankshafts, gears etc.

Shear Stress in Structural Engineering

Structural engineering includes products like fasteners, sealings, beams etc. In these applications to set limits of loading these parts, shear stress is essential.

Shear Stress in Mechanical Engineering

Mechanical engineering means the automotive industry, energy sector, aerospace industry etc. In these fields, safety criteria are important to set for the components of these fields. Shear stress helps in setting these criteria in design and application.

Applications of Shear Stress in Fluid Mechanics

Applications of shear stress in fluid mechanics are discussed below.

Shear Stress in Pipe Flow

It is calculated by

 µ= viscosity of the fluid

du/dy= velocity gradient

Shear stress is important in fluid transportation in a pipe as it provides an expression for the flow as a function of pressure.

Shear Stress in Microfluidic Devices

In Microfluid devices, the shear stress is generated by fluid flow injection. It is important in these devices because it helps in controlling fluid flow and particle behaviour within the small tubes. These devices are commonly used in medical, biological research, environmental monitoring etc.